[자료구조] 힙(heap)이란? - 개념 정리

힙(heap)

힙은 이진트리로서 우선순위 큐(Priority Queue)를 사용하기 위해 만들어진 자료구조이다. 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾을 수 있고, 이진 탐색 트리와는 달리 중복 값을 허용하는 것이 특징이다.

 

힙은 완전히 정렬된 것은 아니지만 그렇다고 정렬이 안된 것도 아니다. 이러한 상태를 느슨한 정렬 상태 또는 반정렬 상태라고 한다.

 

 

힙(heap)의 종류

최소 힙(Min heap)

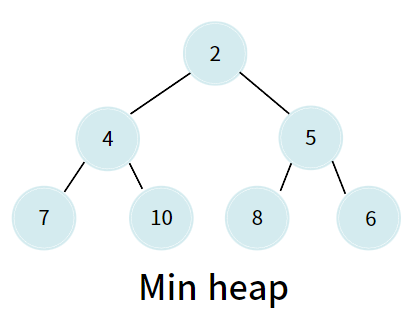
• 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진트리
• 부모 노드의 키 값 ≤ 자식 노드의 키 값

 

최대 힙(Max heap)

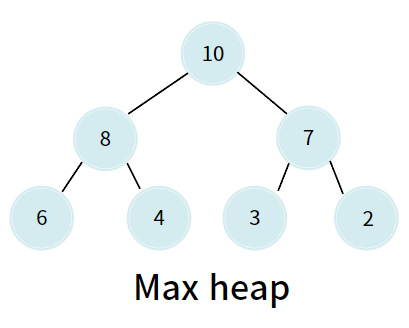
• 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리
• 부모 노드의 키 값 ≥ 자식 노드의 키 값

 

 

힙(heap)의 구현

힙은 배열을 이용하여 구현할 수 있다. 이진트리에서는 각 노드가 최대 2개의 자식 노드를 가질 수 있지만, 배열로 구현한 힙에서는 각 노드가 자식 노드를 최대 2개까지 갖게 된다.

 

또한, 각 노드의 인덱스는 다음과 같이 구할 수 있다.

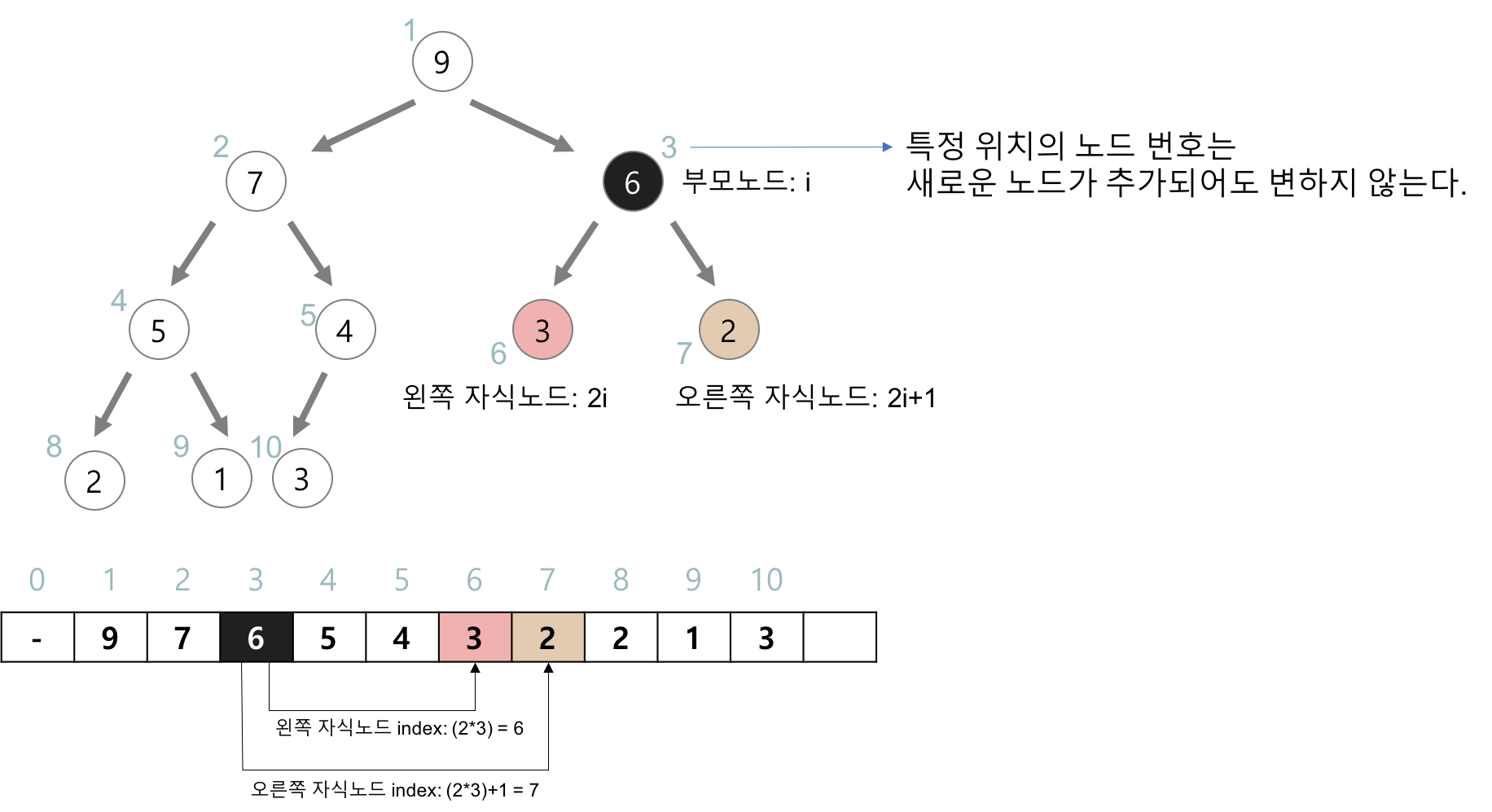
• 부모 노드: i / 2
• 왼쪽 자식 노드: i * 2
• 오른쪽 자식 노드: i * 2 + 1

 

힙의 삽입, 삭제 등의 연산은 일반 이진트리와는 다르게 루트 노드만을 조작하는 것이 아니라, 다른 노드와도 교환하는 과정이 필요하다.

 

힙(heap)의 삽입

힙의 삽입은 다음과 같은 과정을 거친다.

1. 새로운 요소를 힙의 마지막 노드에 이어서 삽입한다.
2. 삽입된 노드를 부모 노드와 비교하여, 부모 노드의 값이 더 작은 경우(최소 힙의 경우) 또는 더 큰 경우(최대 힙의 경우)에 해당 노드와 부모 노드를 교환한다.
3. 교환된 노드와 부모 노드를 다시 비교하여, 더 이상 교환이 필요 없을 때까지 반복한다.

이 과정을 거치면 새로운 요소가 힙의 올바른 위치에 삽입된다.

 

힙(heap)의 삭제

힙의 삭제는 다음과 같은 과정을 거친다.

1. 힙의 루트 노드를 삭제한다.
2. 힙의 마지막 노드를 루트 노드로 옮긴다.
3. 새로운 루트 노드를 기준으로 자식 노드 중 더 작은(최소 힙의 경우) 또는 더 큰(최대 힙의 경우) 값을 가진 노드와 교환한다.
4. 교환된 노드와 자식 노드를 다시 비교하여, 더 이상 교환이 필요 없을 때까지 반복한다.

이 과정을 거치면 힙의 올바른 구조가 유지되면서 루트 노드가 삭제된다.

 

자바 언어를 이용한 힙 구현

public class Heap {
    private int[] heap;
    private int size;

    public Heap(int capacity) {
        heap = new int[capacity];
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public boolean isFull() {
        return size == heap.length;
    }

    public int peek() {
        if (isEmpty()) {
            throw new IndexOutOfBoundsException("Heap is empty.");
        }
        return heap[0];
    }

    public void insert(int value) {
        if (isFull()) {
            throw new IndexOutOfBoundsException("Heap is full.");
        }
        heap[size] = value;
        fixHeapAbove(size);
        size++;
    }

    public int delete(int index) {
        if (isEmpty()) {
            throw new IndexOutOfBoundsException("Heap is empty.");
        }
        int parent = getParent(index);
        int deletedValue = heap[index];
        heap[index] = heap[size - 1];
        if (index == 0 || heap[index] < heap[parent]) {
            fixHeapBelow(index, size - 1);
        } else {
            fixHeapAbove(index);
        }
        size--;
        return deletedValue;
    }

    private void fixHeapAbove(int index) {
        int newValue = heap[index];
        while (index > 0 && newValue > heap[getParent(index)]) {
            heap[index] = heap[getParent(index)];
            index = getParent(index);
        }
        heap[index] = newValue;
    }

    private void fixHeapBelow(int index, int lastHeapIndex) {
        int childToSwap;
        while (index <= lastHeapIndex) {
            int leftChild = getChild(index, true);
            int rightChild = getChild(index, false);
            if (leftChild <= lastHeapIndex) {
                if (rightChild > lastHeapIndex) {
                    childToSwap = leftChild;
                } else {
                    childToSwap = (heap[leftChild] > heap[rightChild]) ? leftChild : rightChild;
                }
                if (heap[index] < heap[childToSwap]) {
                    int temp = heap[index];
                    heap[index] = heap[childToSwap];
                    heap[childToSwap] = temp;
                } else {
                    break;
                }
                index = childToSwap;
            } else {
                break;
            }
        }
    }

    public void printHeap() {
        for (int i = 0; i < size; i++) {
            System.out.print(heap[i]);
            if (i != size - 1) {
                System.out.print(", ");
            }
        }
        System.out.println();
    }

    public int getParent(int index) {
        return (index - 1) / 2;
    }

    public int getChild(int index, boolean left) {
        return 2 * index + (left ? 1 : 2);
    }
}