[이전글]
[ML] 2-1. 머신러닝의 종류 및 적용 사례 (1)
[ML] 2-1. 머신러닝의 종류 및 적용 사례
[이전글] [ML] 1. 머신러닝이란 무엇인가? (About ML: Machine Learning) ittrue.tistory.com/33 [ML] 1. 머신러닝이란 무엇인가? (About ML: Machine Learning) 1. 머신러닝이란? 아서 새뮤얼(Artuhr Samuel, 195..
ittrue.tistory.com
3. 실시간 훈련 여부 구분
3-1 배치 학습(Batch Learning)
배치 학습은 주어진 훈련 세트 전체를 사용하기 때문에 오프라인 환경에서 적합하여 오프라인 학습이라고도 합니다. 먼저, 시스템을 훈련시킨 후 더 이상의 학습 없이 제품 시스템에 적용하는 것입니다. 하지만 이는 컴퓨팅 자원(CPU, GPU, 저장장치 등)이 충분한 환경에서만 사용이 가능하며, 새로운 데이터가 들어오면 처음부터 새롭게 학습해야 하는 단점이 있습니다. 하지만, 이를 해결하기 위해 MLOps 등을 이용한 자동화 기능을 사용하고 있으며, 이후 이전 시스템의 사용을 중지하고 새로운 시스템으로 교체합니다.
3-2 온라인 학습(Online Learning)
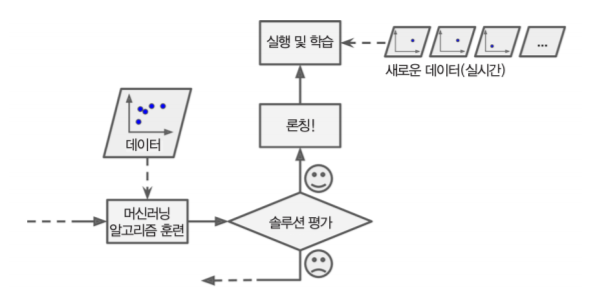
온라인 학습은 하나씩 또는 적은 양의 데이터인 미니 배치(mini-batch)를 사용하여 점진적으로 훈련을 하는 방법입니다. 미니 배치 단위로 학습을 하기 때문에 일반적인 배치 학습에 비해 적은 양의 자원을 사용합니다. 하지만 나쁜 데이터가 주입되는 경우 시스템 성능이 점진적으로 떨어질 수 있기 때문에 지속적인 시스템 모니터링이 필요합니다.
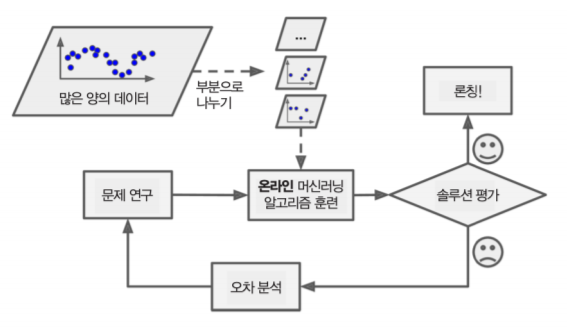
온라인 학습의 예로 주식 가격 시스템 등 실시간 반영이 중요한 시스템을 예로 들 수 있으며, 스마트폰 등 제한된 자원의 시스템, 외부 메모리 학습(매우 큰 데이터셋을 활용하는 시스템) 등에도 활용되고 있습니다. 온라인 학습은 변화하는 데이터에 얼마나 빠르게 적응할 것인지가 중요합니다. 이를 학습률(Learning rate)이라 합니다.
4. 예측 모델 사용 여부 구분
예측 모델 사용 여부는 훈련 모델의 일반화(Generalization) 방식에 따른 분류를 하며, 일반화란 새로운 데이터에 대한 예측을 뜻합니다.
4-1. 사례 기반 학습
사례 기반 학습은 샘플을 기억하는 것이 훈련의 전부입니다. 예측을 위해 기존 샘플과의 유사도를 측정합니다.
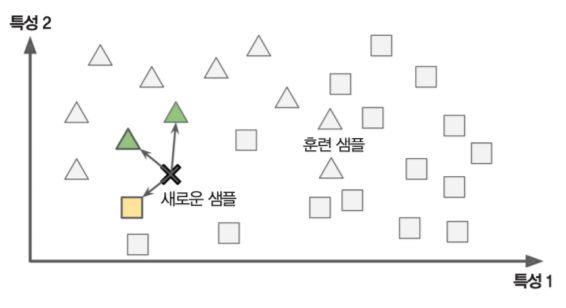
사례 기반 학습의 예로 k-최근접 이웃(k-NN: k-Nearest Neighbors) 알고리즘을 들 수 있습니다. 위 사진을 보면, 새로운 샘플인 X가 기존에 세모인 샘플, 네모인 샘플과의 유사도를 측정하여 유사도가 높은 도형으로 분류하는 것입니다. 위 사진의 경우 새로운 샘플은 세모인 샘플과의 유사도가 더 높게 측정되므로 세모로 분류됩니다.
4-2 모델 기반 학습
모델 기반 학습은 모델을 미리 지정한 후 훈련 세트를 사용해서 모델을 훈련시키는 것입니다. 훈련된 모델을 사용해 새로운 데이터에 대한 예측을 할 수 있으며 앞으로 다룰 대부분의 알고리즘이 모델 기반 학습이라 보시면 됩니다.
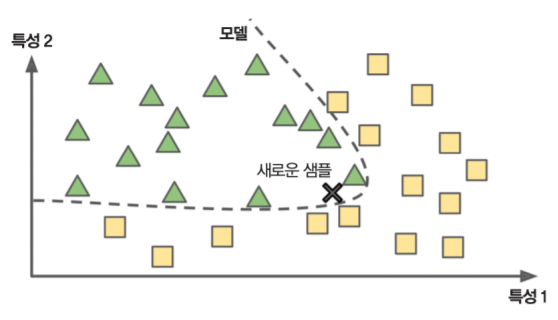
위 사진을 예로 새로운 샘플에 대하여 데이터를 분류하는 방법입니다. 새로운 샘플 X는 모델을 나타내는 점선에 의해 세모에 분류되는 것을 알 수 있습니다.
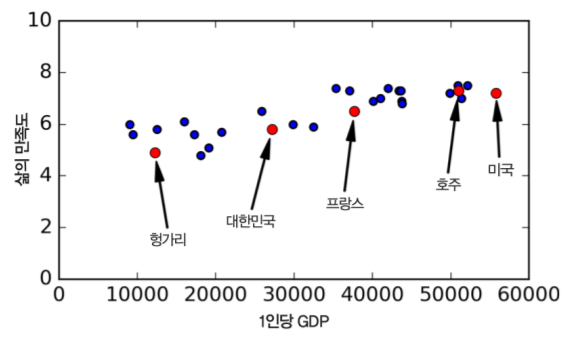
모델 기반 학습의 또 다른 예인 선형 모델 학습으로 OECD 국가의 1인당 GDP와 삶의 만족도 지수 사이의 관계를 파악하는 데 이용할 수 있습니다. 두 지수의 관계를 보면 1인당 GDP가 증가할수록 삶의 만족도가 선형으로 조금씩 증가하는 것처럼 보입니다.
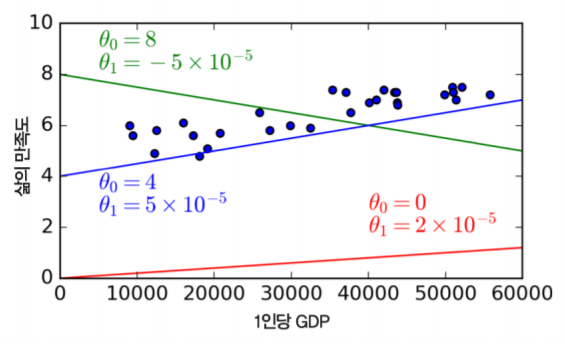
이를 분석하기 위해 데이터를 대표하는 선형 모델(직선)을 찾아야 합니다. 다음과 같은 '삶의 만족도' = θ0 + θ1 × '1인당 GDP' 계산식을 통해 선형 모델 직선을 찾고, 이후 또다시 데이터를 대표할 수 있는 선형 방정식을 찾아야 합니다.
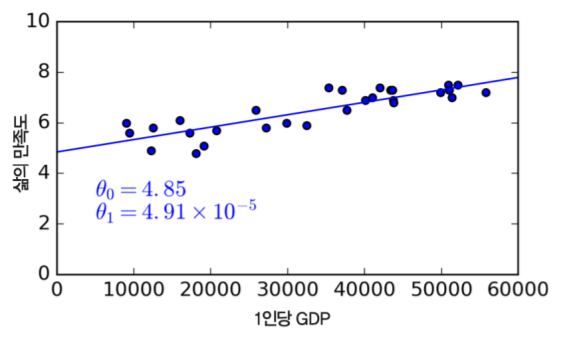
선형 방정식을 찾기 위해서는 성형 회귀 모델을 사용하여 훈련 모델이 알아낸 최적 선형 모델의 절편과 기울기(θ0, θ1)를 이용해 산점도를 그려야 합니다. 위 데이터의 경우 선형 회귀 모델이 절편 θ0는 4.85, 기울기 θ1은 4.91 × 10-5로 구하여 나타낸 직선입니다.
이후 새로운 데이터(임의의 국가의 GDP)를 통해 삶의 만족도를 예측하는 데 사용할 수 있게 됩니다.
[다음글]
[ML] 3-1. 머신러닝의 훈련 조건 (1) - 좋은 데이터와 나쁜 데이터
[ML] 3-1. 머신러닝의 훈련 조건 (좋은 데이터와 나쁜 데이터)
[이전글] [ML] 2-2. 머신러닝의 종류 및 적용 사례 (2) ittrue.tistory.com/36 [ML] 2-2. 머신러닝의 종류 및 적용 사례 (배치 학습, 온라인 학습, 사례 기반 학습, 모델 기반 학습) [이전글] [ML] 2-1. 머신러닝..
ittrue.tistory.com
'Computer Engineering > 머신러닝(ML: Machine Learning)' 카테고리의 다른 글
| [ML] 4-1. 머신러닝에서의 하이퍼파라미터란 무엇일까? (파라미터 vs 하이퍼파라미터) (0) | 2021.05.08 |
|---|---|
| [ML] 3-2. 머신러닝의 훈련 조건 (과대적합과 과소적합) (0) | 2021.04.24 |
| [ML] 3-1. 머신러닝의 훈련 조건 (좋은 데이터와 나쁜 데이터) (0) | 2021.04.24 |
| [ML] 2-1. 머신러닝의 종류 및 적용 사례 (지도 학습, 비지도 학습, 준지도 학습, 강화 학습) (0) | 2021.04.14 |
| [ML] 1. 머신러닝이란 무엇인가? (About ML: Machine Learning) (0) | 2021.04.10 |